Plant Energy Transductions-1
The Sun provides the energy required for the Earth; http://www.bio.miami.edu/
Principles of Thermodynamics
Thermodynamics is the study of energy and its transformations. Before launching into it, it is worth briefly considering what energy is, as it is not as obvious as you might think. As Richard Feynman puts it, “you can think of energy as something akin to children's building blocks. Say you have ten bricks. You let the kid play with them, and then notice that there are only eight lefts. You're slightly worried until you notice that there is a suspicious lump under the sheets of his bed, which looks just like two blocks. Ah ha, you think, I still have ten blocks. Whilst doing this, three more blocks are secreted by the kid. You hunt about, and then notice that the level of water in the bath is slightly higher, just sufficient to account for the volume of the three blocks. Then you notice a smell of burning and another missing block, but by checking the carbon dioxide concentration in the air, you deduce that the little brat has burnt one of the blocks. And so on. Energy is rather like the building blocks, in that you know you have a certain amount of it that never changes, BUT, in reality there are NO literal, concrete building blocks in nature: energy never exists in some 'pure' unadulterated form: it always exists as clever mathematical trickery of the volume displacement, air composition and suspicious lumpiness varieties”.
Energy therefore can take many forms, none of them are more fundamental than the others. It can usually be expressed as the multiplication of a potential factor by a capacity factor. For example, the energy E, required to compress a gas by a certain volume (capacity factor) ∆V (where ∆ means’ a change in') is simply E = p∆V where p is the pressure of the gas you are trying to compress (potential factor). Similarly, the energy you can release from moving a certain amount of charge ∆Q towards an opposite charge producing an electric field of strength E, is E∆Q. The osmotic equivalent is to move a certain mass (M) of molecules with an osmotic potential (C) is E = C∆M; the heat equivalent is to change the entropy (S) of a gas at a certain temperature (T) is E = T∆S; and so on. These are the 'block counting' mechanisms we have. Ultimately, as Einstein showed, energy and mass are same things: the energy extractable from a system is equal to its mass multiplied by the speed of light squared, E = m c2. However, even when considering quite large energy changes, the change in mass is so small as to be negligible, which is why the conservation of energy (the fact that the energy extractable from a system equals the energy originally put into it), and the conservation of mass (mass in = mass out) have traditionally been considered separate laws. In fact they are both approximations to the conservation of mass-energy.
Energy can be loosely defined as the ability of a system to do work on its surroundings. Work means moving things, deforming things, breaking things, etc.
Thermodynamics has four important laws, which we will take on at a time. The first is actually called the ‘zeroeth’, as it got tacked on as an after-thought.
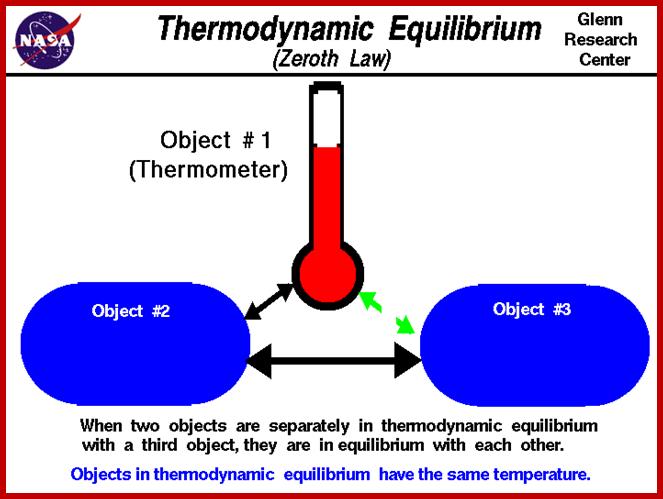
Zeroeth law
If a system A is in thermodynamic equilibrium with system B, and system B is in thermodynamic equilibrium with system C, then A is also in equilibrium with C. Put more plainly, if A = B and B = C then A = C too (commonsense).
First law
Energy can be neither created nor destroyed: it can only change form. You cannot win by making energy from nothing: you can only break even.
There are several ways to express the first law, and physicists and chemists often use different conventions. The prevalent mathematical way, and the one of the most important to thermodynamics, which deals primarily with work and heat exchanges, is:
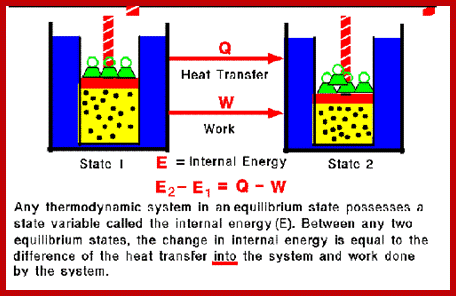
U = Q + W
The internal energy (U) of a system is the heat in the system (Q) plus the work (W) previously done on the system. Using 'delta' notation for changes in energy, where
∆X = Xafter − Xbefore
Changes in internal energy can be expressed as:
∆U = ∆Q + ∆W
The change in internal energy is the heat supplied to the system, plus the work done on the system (note the positive signs). This is more convenient, since the absolute value of the internal energy is extremely difficult to measure with any accuracy (ultimately, it is mc2, but you'd need to know the mass in kilograms to an accuracy of about fifteen decimal places to get the answer in Joules to any reasonable degree of accuracy).
Physicists, with their "W is work done by the system" convention may write the first law as:
∆U = ∆Q − ∆W
The internal energy is termed a state function: this means that its value is independent of the history of the system. That is to say, it doesn't matter how the energy was supplied (heat or work), a system that has had 10 J (Joules, the SI energy unit) of heat energy supplied to it will experience the same change in internal energy as a system that has had 5 J of heat supplied and 5 J of work done on it. Other thermodynamic functions of state include entropy, enthalpy and free energy, which we will cover shortly.
A concept closely related to internal energy is that of enthalpy, H. When a reaction is done on Earth in an open vessel (like a test tube, conical flask, etc.), the reactants may well have a different volume to the products. If the products are more voluminous than the reactants, a certain amount of energy will be 'wasted' pushing the atmosphere away; and if the volume decreases, a certain amount of work will be done on the system as the atmosphere squashes it. The change in enthalpy of the system is the change in internal energy plus the work done on the system by the atmosphere (if it is squashed), or less the work done on the system (if it expands). That is to say, enthalpy change is the energy exchanged as heat (∆Q) between system and surroundings once you've accounted for any energy lost by shifting the atmosphere out of the way. The mechanical work done on the atmosphere is −p∆V (using our convention that work done by the system is negative), i.e. atmospheric pressure (p) times the increase in volume of the system (∆V). If we define ∆H as ∆Q under constant pressure, then:
∆H = ∆U + p∆V
A reaction that leads to a decrease in enthalpy (∆H < 0) will release heat to the surroundings, and is termed exothermic. A process that increases the enthalpy of the system (∆H > 0) will be positive in sign, and hence will take up energy from the surroundings, and is termed endothermic. Exothermic reactions tend to be more favored than endothermic reactions because low energy states are more stable. Note that for a reaction to be exothermic, the system must lose internal energy (∆U is negative) and/or contract in volume (∆V is negative). No heat will be evolved during a chemical reaction if the liberated internal energy is entirely used up in pushing the atmosphere away.}
Second law
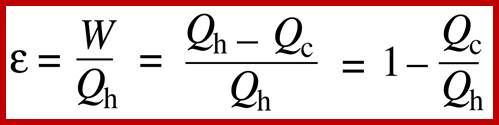
Heat is a specially degraded form of energy, and is difficult to convert to useful, workable energy. The efficiency of a process measures how well it converts forms of energy amongst each other. In particular, the efficiency of converting heat to work is related to the temperature of the heat sink to which the heat gets dumped. You can only break even in heat/work conversion if your heat sink is at absolute zero. Another way to express the second law is that the entropy (i.e. the amount of disorder) of the universe is increased by all energy-conversion processes: they all produce some amount of heat, which cannot be converted back to useful energy without an absolute zero (0 Kelvin) heat sink.
The efficiency, η, of converting heat to work is related to the temperatures of the heat source (e.g. a plane engine) and heat sink (e.g. the atmosphere). This is maximally:
η = ( Tsource − Tsink ) ⁄ Tsource
Where ‘T is the absolute temperature, in Kelvin terms; Note that if the sink is at absolute zero, (0 K, or −273.15°C), the efficiency will be 1, i.e. 100%. This is a convenient way to understand why the second law says you can only break even (i.e. convert heat to work with 100% efficiency) with a sink at absolute zero. The commoner way of expressing the second law is in terms of entropy. Entropy, S, is the amount of disorder in a system, technically:
S = k ln W
Where W is the number of ways of arranging the heat energy in the system, and k is Boltzmann's constant (1.380650 × 10−23 J K−1). The amount of disorder in the universe is always increased by physical processes:
∆Suniverse = ∆Ssystem + ∆Ssurroundings > 0
Gibbs free energy:
The best known of the free energy equations is that of Gibbs:
∆G = ∆H − T∆S
∆G is the (change in) Gibbs free energy of the system, which can be used to describe changes in free energy in constant pressure systems (such as biological systems), and is the most important term for biologists, as it determines whether a reaction is feasible. Helmholtz free energy (A for Arbeit) is the constant volume version (∆A=∆U −T∆S). A reaction with negative ∆G is termed exergonic, and will be spontaneous, although it may not occur at any appreciable rate. One with positive ∆G is termed endergonic, will not be spontaneous, and will not go ahead, unless coupled to another reaction with negative ∆G (biology does this all the time, by coupling the hydrolysis of ATP (very exergonic) to thermodynamically unfavorable reactions).
Note that you could write out Gibbs energy in full as:
∆G = ∆U + p∆V − T∆S
∆G is the maximum quantity of useful work that a chemical reaction can perform on its surroundings (∆G = −Wmax). ∆U can be thought of as the total energy liberated by a chemical reaction.
The standard free energy change, ∆G0 is defined as the free energy change associated with e.g. the reaction:
A + B ⇌ C + D
when the temperature is 298 K (25°C), the pressure 1 atmosphere (101 325 Pa), and A, B, C and D are all at 1 M concentrations. This is actually a bad idea for biology, since water (55.5 M) and proton concentration (10−7 M at pH 7) are almost never at this standard value. Hence, ∆G0′ has been defined to account for this: it assumes water as a 55.5 M solvent, at pH 7.
If we set up a reaction under ∆G0 (or ∆G0′) conditions, and we find it has a positive sign, we know the forward reaction will not be energetically favored with these concentrations of products and reactants. However, the reverse reaction has the same value of ∆G0 but the opposite sign, hence the reverse reaction will be favored.
So, if ∆G0 has negative sign, we know that (under standard conditions) the forward reaction is feasible, and A and B will convert (at some rate) to C and D. This means the product and reactant concentrations will change over time. To work out the ∆G under these new concentration conditions, we need to use the formula:
∆G = ∆G0 + R T ln Q
Where R is the universal gas constant (8.314472 J K−1 mol−1), T the absolute temperature, and Q is the mass action ratio. This is calculated by multiplying together the molar concentrations of the products and dividing them by the molar concentrations of the reactants multiplied together (i.e., product of the products divided by the product of the reactants):
A + B ⇌ C + D
Q = [C] [D] ⁄ [A] [B]
Let's start with the ∆G0 reactant and product concentrations, all 1 M, and let the reaction run. As the reactant and product concentrations change during the course of the reaction (starting from the ∆G0 conditions), ∆G will change as Q changes, and will head towards zero. If ∆G0 is negative, the forward reaction is favored, and Q will increase (products produced at expense of reactants), so making ∆G less negative. If however ∆G0 is positive, the backwards reaction is favored, and Q will decrease, so making ∆G less positive. At some combination(s) of product and reactant concentrations, a dynamic equilibrium will be achieved, where neither net forward nor net backwards reaction is favored, and ∆G = 0. Under these conditions:
∆G = ∆G0 + R T ln Q = 0
∆G0 = − R T ln Keq
where the value of Q is a special one called the equilibrium constant, Keq:
Keq = Qeq = [C]eq [D]eq ⁄ [A]eq [B]eq
At this equilibrium point, no net reaction will occur. A very high Keq indicates that the reaction proceeds to completion, i.e. the concentration of products at equilibrium vastly exceeds the residual reactant concentrations.
Note that we can combine the two equations above:
∆G = ∆G0 + R T ln Q
∆G0 = − R T ln Keq
∆G = R T ln Q − R T ln Keq = − R T ln ( Keq ⁄ Q )
This shows clearly that the free energy change is negative (spontaneous reaction) only if Q is less than Keq, i.e. when there is an excess of product over reactant (w.r.t. the equilibrium values). We can also write this as:
∆G = R T ln ( Q ⁄ Keq )
Third law
The entropy of a perfect crystal at absolute zero is 0. There is no physical process whereby absolute zero can be achieved; hence you cannot have a heat sink at 0 K. Therefore, you cannot break-even: you can only lose.
http://www.grc.nasa.gov/
This one doesn't have too much relevance to biology, beyond nailing down the fact that the second law hinted strongly at: the first law says you can't win (i.e. make energy from nothing), the second law says you can't break even except with a heat sink at 0 K, and the third law says that you can't even do that, since 0 K is unattainable. Rather a depressing triplet.
The application of thermodynamics to biology has important implications in determining which reactions are feasible (i.e. spontaneous) and which can be made spontaneous by coupling them to another process (e.g. the exergonic hydrolysis of ATP).
Refer to Biochemistry/Steve’s’ Thermodynamics.htm; it is an excellent piece of Text one loves to read.

http://advchem-niva.wikispaces.com/


www.theory.physics.manchester.ac.uk
First Law:
www.wright.nasa.gov
First Law; www.splung.com
Second Law: